You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Paravane stabilisers actual loads.
- Thread starter Simi 60
- Start date
The friendliest place on the web for anyone who enjoys boating.
If you have answers, please help by responding to the unanswered posts.
If you have answers, please help by responding to the unanswered posts.
mvweebles
Guru
- Joined
- Mar 21, 2019
- Messages
- 7,778
- Location
- United States
- Vessel Name
- Weebles
- Vessel Make
- 1970 Willard 36 Trawler
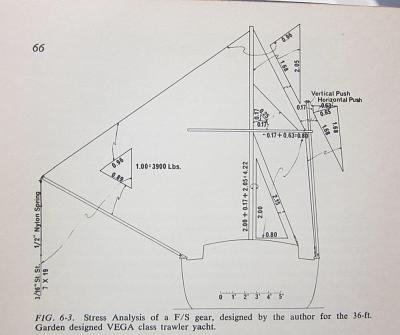
Here’s a stress analysis from one of Beebe’s books that should help calculating some loads.
Any idea how to interpret this? If I understand correctly at notation "1.00 = 3990 lbs," means that this value calcuated for a 36-foot Vega (a Seaton adaptation to my Willard 36), then compression on mast is "4.22." Does that mean compression is 4.22 x 3990, or over 16k lbs???? I note that he spec's a 1/2" nylon line tether - modern 1/2" nylon rope has a breaking strength of around 5500 lbs, SWL of one-quarter that. I'd guess ropes of today are a bit stronger than the ones of 50-years ago.
Interesting.....
Peter
Jeff F
Guru
- Joined
- Nov 5, 2015
- Messages
- 2,554
- Location
- Canada
- Vessel Name
- Escapade
- Vessel Make
- 50` US Navy Utility trawler conversion
I'd bet the spec on nylon is deliberate, to absorb shock loadings as much as possible and build in a bit of a spring.
Your reading seems correct. This notation seems consistent with my theory - the 3990 would be the max force from the fish.
Your reading seems correct. This notation seems consistent with my theory - the 3990 would be the max force from the fish.
I'd bet the spec on nylon is deliberate, to absorb shock loadings as much as possible and build in a bit of a spring.
Your reading seems correct. This notation seems consistent with my theory - the 3990 would be the max force from the fish.
I think you’re right on the nylon. Tom Davenport, who designed the paravanes for most of the KK42s that had paravanes, included 8’x1/2” nylon in all of them. I know on ours, you could watch it stretch and it did smooth out the ride.
I interpreted the loading same as Jeff. It is a lot.
Jeff F
Guru
- Joined
- Nov 5, 2015
- Messages
- 2,554
- Location
- Canada
- Vessel Name
- Escapade
- Vessel Make
- 50` US Navy Utility trawler conversion
Thinking this through... As force increases on the fish, the effective angle of attack increases. At some point the lift is going to disappear or be severely decreased as the foil stalls. That's the 3990.
Does that make sense? I can imagine if that happened the fish might come to the surface.
I'm wondering what happens when the force exceeds design. Matching fish to structure seems key here.
Does that make sense? I can imagine if that happened the fish might come to the surface.
I'm wondering what happens when the force exceeds design. Matching fish to structure seems key here.
hollywood8118
Guru
- Joined
- Nov 16, 2009
- Messages
- 2,393
- Location
- USA
- Vessel Name
- " OTTER "
- Vessel Make
- Ocean Alexander Europa 40
I feel the last few posts are correct in the calculated loads that the fish can exert on the rig. At some point the load can exceed the hydrodynamic effort of the angle of attack of the fish and it can be "pulled upward" effectively stalling the fish, that is one load that can be calculated to a speed number. But, additional loading can occur if the fish strikes an object, or as I have personally have had the pleasure of striking a large log and dragging it which no doubt far exceeded the load the fish could.. it was a BIG log and we were at 8kts of boat speed. The nylon line ( mine was 5/8") definitely stretched but did not break. Ironically I didn't notice the change in motion or the boat pulling to the right because the autopilot was correcting for the asymmetrical pull. I did notice the constant left rudder on the autopilot screen and the slight drop in speed and that's how I was alerted.
The nylon link in the system is designed to part before the rig hits its maximum yielding point and collapses, and it also is a shock absorber.
Personally I like the simplicity of paravanes as you can see its operation and it has very few parts to break and is simple to fit. I looked at a new active stabilizer system being installed on a high speed boat this week and was surprised to see the fins were made of UHMW or some type of flexible plastic as part of its fail safe.
HOLLYWOOD
The nylon link in the system is designed to part before the rig hits its maximum yielding point and collapses, and it also is a shock absorber.
Personally I like the simplicity of paravanes as you can see its operation and it has very few parts to break and is simple to fit. I looked at a new active stabilizer system being installed on a high speed boat this week and was surprised to see the fins were made of UHMW or some type of flexible plastic as part of its fail safe.
HOLLYWOOD
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
Going down a rabbit hole this morning I used an online calculator to estimate the forces of a 300 square inch delta wing in seawater.
The basic formula to calculate lift on a wing from NASA:
An aircraft's lift capabilities can be measured from the following formula: L = (1/2) d v2 s CL. L = Lift, which must equal the airplane's weight in pounds. d = density of the air. This will change due to altitude [fluid density].
My values and assumptions:
CL = 0.75 Notes: Coefficient of Lift was determined by splitting the difference of the CL(Max) for a delta wing of an airplane. I couldnt find relevant data for a paravane fish
d = 1.025 Notes: The density of seawater is 1.02 to 1.03. I split the difference.
s = 300 sq inches. I took this from Kolstrad's website for their medium fish intended for boats 50' - 60'
V = 8 knots or 4.11 M/s
The resulting lift calculations:
= 1260.0876568539 newton
= 126008765.68539 dyne
= 128493.18134672 gram force
= 1260.0876568539 kilogram-meter/second^2
= 128.49318134672 kilogram force
= 0.28327897435034 kip
= 283.27897404848 pound force
= 9114.2314757625 poundal
Again, these are assumptions and I am by no means an aeronautical or marine engineer. I'm just trying to understand more about the actual forces on a 300 sq inch plywood wing dragged through seawater at 8 knots.
One note: The poundal is defined as the force necessary to accelerate 1 pound-mass at 1 foot per second. I'm not sure I full understand this concept.
Would love some feedback, holes poked, etc.
The basic formula to calculate lift on a wing from NASA:
An aircraft's lift capabilities can be measured from the following formula: L = (1/2) d v2 s CL. L = Lift, which must equal the airplane's weight in pounds. d = density of the air. This will change due to altitude [fluid density].
My values and assumptions:
CL = 0.75 Notes: Coefficient of Lift was determined by splitting the difference of the CL(Max) for a delta wing of an airplane. I couldnt find relevant data for a paravane fish
d = 1.025 Notes: The density of seawater is 1.02 to 1.03. I split the difference.
s = 300 sq inches. I took this from Kolstrad's website for their medium fish intended for boats 50' - 60'
V = 8 knots or 4.11 M/s
The resulting lift calculations:
= 1260.0876568539 newton
= 126008765.68539 dyne
= 128493.18134672 gram force
= 1260.0876568539 kilogram-meter/second^2
= 128.49318134672 kilogram force
= 0.28327897435034 kip
= 283.27897404848 pound force
= 9114.2314757625 poundal
Again, these are assumptions and I am by no means an aeronautical or marine engineer. I'm just trying to understand more about the actual forces on a 300 sq inch plywood wing dragged through seawater at 8 knots.
One note: The poundal is defined as the force necessary to accelerate 1 pound-mass at 1 foot per second. I'm not sure I full understand this concept.
Would love some feedback, holes poked, etc.
Last edited:
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
One other interesting note. Delta shaped wings stall at high AOA and low CL(max). In aircraft the delta wing characteristics means landing requires a high angle of attack or a higher speed landing. If I understand this correctly - at low speeds a delta wing shaped "fish" would stall at a fairly low AOA.
Last edited:
Xlantic
Guru
A lot lower than the other numbers in earlier posts. Difference could have to do with steady-state vs shock loads.
For example, when I am lifting my flopper-stoppers out of the water and on to the boat I have to do it slowly as the downward force increases tremendously the faster I try to pull.
For example, when I am lifting my flopper-stoppers out of the water and on to the boat I have to do it slowly as the downward force increases tremendously the faster I try to pull.
Last edited:
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
Hmmm....if I had a 300 sq in fish and that crane scale KnotYet mentioned I could test this underway using our main mast boom.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
A lot lower than the other numbers in earlier posts. Difference could have to do with steady-state vs shock loads.
For example, when I am lifting my flopper-stoppers out of the water and on to the boat I have to do it slowly as the downward force increases tremendously the faster I try to pull.
Yes, the lift calculations aren't the same as force required to overcome drag of the fish as the fish is pulled up or through (like a sea anchor) the water.
Last edited:
If you end up trying that, get this baby:Hmmm....if I had a 300 sq in fish and that crane scale KnotYet mentioned I could test this underway using our main mast boom.
https://www.amazon.com/dp/B09F5W2LTQ/ref=syn_sd_onsite_desktop_58?ie=UTF8&psc=1&pd_rd_plhdr=t
Under $100 and 1000kg capacity!
Simi 60
Guru
- Joined
- Jul 1, 2016
- Messages
- 5,482
- Location
- Australia
- Vessel Make
- Milkraft 60 converted timber prawn trawler
Going down a rabbit hole this morning
= 128.49318134672 kilogram force
= 283.27897404848 pound force
Again, these are assumptions and I am by no means an aeronautical or marine engineer. I'm just trying to understand more about the actual forces on a 300 sq inch plywood wing dragged through seawater at 8 knots.
.
Thanks for that and sort of what I was thinking
Simi 60
Guru
- Joined
- Jul 1, 2016
- Messages
- 5,482
- Location
- Australia
- Vessel Make
- Milkraft 60 converted timber prawn trawler
Originally Posted by Xlantic View Post
A lot lower than the other numbers in earlier posts. Difference could have to do with steady-state vs shock loads.
For example, when I am lifting my flopper-stoppers out of the water and on to the boat I have to do it slowly as the downward force increases tremendously the faster I try to pull.
Yes, the lift calculations aren't the same as force required to overcome drag of the fish as the fish is pulled up or through (like a sea anchor) the water.
But surely the load would be no more than what it gets being dragged through water at the 8 knot calculated speed.????
I would think there would be a point where no more force could be made.
The only way to get more force/loading would be to increase the size of the fish
Or the density of the material it is being dragged through.
Add: But thinking further speed would effect it to a degree
Thinking along the lines of tie a boat to a dock and accelerate slowly to a set speed
Vs
Accelerate like a madman and hit the end of the rope - bang
But even on a roll, is it really going to be ripped/rolled through the water more than 8 knots?
And there is no sudden stop at the end.
And there is nylon or springs to take the hit.
Last edited:
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
Going a little further here. Assuming it's really "only" 283 pounds at the fish then calculating the ft-lbs (torque) at the center end of the lever (6 meters or 19 feet at center mast to the end of an extended pole) you get 5567 ft-lbs. So there would be 5567lbs of rotational force (in one direction) on the center of the rigging from one 300 sq in fish.
MoF = F * L
Where MoF is the moment of force (N*m)
F is the total force (N)
L is the total length (m)
MoF = F * L
Where MoF is the moment of force (N*m)
F is the total force (N)
L is the total length (m)
Last edited:
In response to your opening line, drag in a fluid increases to the square of speed.But surely the load would be no more than what it gets being dragged through water at the 8 knot calculated speed.????
I would think there would be a point where no more force could be made.
The only way to get more force/loading would be to increase the size of the fish
Or the density of the material it is being dragged through.
Add: But thinking further speed would effect it to a degree
Thinking along the lines of tie a boat to a dock and accelerate slowly to a set speed
Vs
Accelerate like a madman and hit the end of the rope - bang
But even on a roll, is it really going to be ripped/rolled through the water more than 8 knots?
And there is no sudden stop at the end.
And there is nylon or springs to take the hit.
A fish that adds 50 lbs of load at 1 kt will add 500 lbs at 10 kts. The roll
motion being transmitted to the fish is in addition to the boat speed also already present.
That roll motion is magnified by the 20 ft or so of outrigger so perhaps 4x
faster than whatever roll you are experiencing at the helm or elsewhere
on the boat. The few knots of roll you feel produce large forces at the fish, as you can imagine.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
That roll motion is magnified by the 20 ft or so of outrigger so perhaps 4x
faster than whatever roll you are experiencing at the helm or elsewhere
on the boat. The few knots of roll you feel produce large forces at the fish, as you can imagine.
This is what I've been trying to get my head around. If a plywood fish or even a plate galvanized steel fish was under the forces often described (3990 lbs) would it not break or buckle? As I've been able to understand it...the fish themselves, traveling through seawater at 8 knots at an (assumed) max coefficient of lift will produce under 300 lbs of force. Too much of an angle of attack means they stall and dump their lift.
However, when you look at the torque that <300 lbs creates back at the center of the ship it's 5500 ft-lbs per fish or 11,000 lbs total.
So my question then is does the torque of about 11,000 ft-lbs transfer through the topping lifts into the poles themselves, the central mast or A-frame as a compression force?
I'm assuming yes.
If yes, then your rig needs to be constructed in a way to distribute that 11,000 lb load across the house deck, down through walls or bulkheads or stantions with enough strength as to eliminate deformation of the structure itself.
For perspective if you applied 10,000 lbs to the center of a 4" square aluminum tube with a .25" wall thickness it will deform 0.5" across a ten foot span.
I suspect we often confuse the torque at the end of the arm with the force on the fish themselves which is why confirming the force on a fish is key to a better understanding (and the related calculations of loads) for anyone considering paravanes.
Now, I fully acknowledge that this doesn't align with Beebe's diagram but I also don't know how he calculated his design. No matter, my proposal could be full of barnacles.
OK, so who has a 300 sq-in fish I can drag around the Salish Sea with a Crane Scale attached to it?

Last edited:
hollywood8118
Guru
- Joined
- Nov 16, 2009
- Messages
- 2,393
- Location
- USA
- Vessel Name
- " OTTER "
- Vessel Make
- Ocean Alexander Europa 40
Another factor that may have an effect is the acceleration and deceleration of the fish as they swing through the arc as the pole rises and falls. Also the speed of the fish is not static even if the boat speed is.. so I think the load changes there also.
I'm no ingineer but I stood next to one once!
Hollywood
I'm no ingineer but I stood next to one once!
Hollywood
Jeff F
Guru
- Joined
- Nov 5, 2015
- Messages
- 2,554
- Location
- Canada
- Vessel Name
- Escapade
- Vessel Make
- 50` US Navy Utility trawler conversion
Going a little further here. Assuming it's really "only" 283 pounds at the fish then calculating the ft-lbs (torque) at the center end of the lever (6 meters or 19 feet at center mast to the end of an extended pole) you get 5567 ft-lbs. So there would be 5567lbs of rotational force (in one direction) on the center of the rigging from one 300 sq in fish.
MoF = F * L
Where MoF is the moment of force (N*m)
F is the total force (N)
L is the total length (m)
Just as a reference point, the Seakeeper 3 produces about 7,800 n-m maximum rotational force. Not sure how that squares with your numbers, but that's probably somewhere close to properly designed paravanes for that boat.
300 pounds seems light as a max. We want the force required to get to stall.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
Another factor that may have an effect is the acceleration and deceleration of the fish as they swing through the arc as the pole rises and falls. Also the speed of the fish is not static even if the boat speed is.. so I think the load changes there also.
I'm no ingineer but I stood next to one once!
Hollywood
Agreed and I haven't even stood next to one
I did try and calc the loads at CL(Max) for a 300 sq-in delat wing in seawater but there are some unkowns for sure.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
Just as a reference point, the Seakeeper 3 produces about 7,800 n-m maximum rotational force. Not sure how that squares with your numbers, but that's probably somewhere close to properly designed paravanes for that boat.
300 pounds seems light as a max. We want the force required to get to stall.
Interesting. 7800 n-m is 5752 ft-lbs so yeah, it's ballpark.
Delfin
Grand Vizier
- Joined
- Jan 20, 2010
- Messages
- 3,850
The load on the fish is much smaller than the load on the hull connection points and mast rigging.
The force gets multiplied by the distance from the roll center.
A few hundred pounds on a 25' lever will produce a tremendous righting force.
Do you recall Archimedes' famous quote?
Doesn't a lever require a fulcrum for your analogy to be correct? Without a fulcrum, I believe the load would be the same when measured at the fish or the attachment point.
Jeff F
Guru
- Joined
- Nov 5, 2015
- Messages
- 2,554
- Location
- Canada
- Vessel Name
- Escapade
- Vessel Make
- 50` US Navy Utility trawler conversion
Very interesting. But I don't understand why Beebe would specify 4000 pounds or that line size if the fish gave up at 300 pounds. I get safety factors, but this doesn't quite fit my intuitive model.Interesting. 7800 n-m is 5752 ft-lbs so yeah, it's ballpark.
Jeff F
Guru
- Joined
- Nov 5, 2015
- Messages
- 2,554
- Location
- Canada
- Vessel Name
- Escapade
- Vessel Make
- 50` US Navy Utility trawler conversion
Going a little further here. Assuming it's really "only" 283 pounds at the fish then calculating the ft-lbs (torque) at the center end of the lever (6 meters or 19 feet at center mast to the end of an extended pole) you get 5567 ft-lbs. So there would be 5567lbs of rotational force (in one direction) on the center of the rigging from one 300 sq in fish.
Rereading this. I *think* the rotational force would have to be measured at the center of rotation for the boat, which would be farther from the end of the pole. Somewhere low in the hull, I would think.
Happy to be corrected by someone who knows something
Simi 60
Guru
- Joined
- Jul 1, 2016
- Messages
- 5,482
- Location
- Australia
- Vessel Make
- Milkraft 60 converted timber prawn trawler
Doesn't a lever require a fulcrum for your analogy to be correct? Without a fulcrum, I believe the load would be the same when measured at the fish or the attachment point.
It's what I was thinking
Load on rope is load on rope
It shouldn't increase because it's held outboard by a stick
Doesn't a lever require a fulcrum for your analogy to be correct? Without a fulcrum, I believe the load would be the same when measured at the fish or the attachment point.
Torque is defined as force at a distance, i.e, increase either one and youIt's what I was thinking
Load on rope is load on rope
It shouldn't increase because it's held outboard by a stick
increase the force. If the fish was attached only to the rail it would have
little effect on righting the boat's motion. That same fish 20' further away
now exerts a much stronger force where the 'stick' attaches.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
As I understand it the fulcrum is the center of the rig and yes the length of poles plus half the beam multiplies the force of 300 lbs by a LOT. Anyone who's thrown a length of pipe on a breaker bar knows this intuitively.
The test we need is what KnotYet proposed. Hook up a scale to a fish and measure it at different speeds/angles. Until then it's all models and assumptions.
The test we need is what KnotYet proposed. Hook up a scale to a fish and measure it at different speeds/angles. Until then it's all models and assumptions.
There are at least 2 errors in my post above.In response to your opening line, drag in a fluid increases to the square of speed.
A fish that adds 50 lbs of load at 1 kt will add 500 lbs at 10 kts. The roll
motion being transmitted to the fish is in addition to the boat speed also already present.
That roll motion is magnified by the 20 ft or so of outrigger so perhaps 4x
faster than whatever roll you are experiencing at the helm or elsewhere
on the boat. The few knots of roll you feel produce large forces at the fish, as you can imagine.
The '50 lbs' of load at 1 kt should read '5 lbs' and I believe that rather than
getting multiplied by 100 it would only be multiplied by 81, the square of the
difference in speed, so the load at 10 kts should read 405 lbs.
Gdavid
Guru
To further confuse the subject, keep in mind that this is a dynamic situation rather than static. Balancing a force diagram in a static situation is rather straightforward because nothing moves and the forces have to balance out. In a dynamic situation, the forces do not balance out, instead, the objects move. Eventually everything will reach an equilibrium, or close to it and you are now looking at static situation but once you start talking about the boat rolling and the bird being lifted up while being pulled forward, you are in a dynamic situation again.
When the bird produces tension in the line, the end of the pole will drop, lowering the tension and thus decreasing the pull of the bird. The rate at which the pole drops is complex and difficult to calculate, but it is clear that the reaction of the boat depends on the weight and inertia of the boat.
When the bird produces tension in the line, the end of the pole will drop, lowering the tension and thus decreasing the pull of the bird. The rate at which the pole drops is complex and difficult to calculate, but it is clear that the reaction of the boat depends on the weight and inertia of the boat.
Airstream345
Guru
- Joined
- Jul 3, 2017
- Messages
- 1,016
- Location
- United States
- Vessel Name
- FORTITUDE
- Vessel Make
- Kadey Krogen 54-8
This is the big question in Beebe's design and many of the assumptions about the forces involved. as Simi pointed out "500 lbs is 500 lbs"....so it's the torque of that 500 lbs out on a long lever. Think of a seesaw...it doesn't get heavier at the fulcrum if you put a 250 lb weight on either end.
The more I think about this the more I'm beginning to consider it's about the torque on the rig and transfering that to the vessel. So in my theorical model it's not pushing down on the deck with 11,000 lbs of force rather it 5500 ft-lbs of torque for each side going in and our of perfect equilibirum (seesaw example)
The more I think about this the more I'm beginning to consider it's about the torque on the rig and transfering that to the vessel. So in my theorical model it's not pushing down on the deck with 11,000 lbs of force rather it 5500 ft-lbs of torque for each side going in and our of perfect equilibirum (seesaw example)
Attachments
Last edited:
Similar threads
- Replies
- 8
- Views
- 1K
- Replies
- 4
- Views
- 2K